Modified Growth Rates

The modified growth rates shown below are computed via

\[ \omega(k;\epsilon) = k\Big( \epsilon_\rho\,\mathrm{Im}\,c^{(0)}_1(k) \;+\; \epsilon^2\,\mathrm{Im}\,c^{(2)}(k) \Big), \]

where the first term is the classical Miles growth rate ($\epsilon_{\rho} \text{Im } c_1^{(0)}$ comes from another asymptotic expansion, to approximate $\text{Im }c^{(0)}$) and the second term is the leading-order modification dependent on the wave-induced mean flow $U^{(2)}(b)$ (the dispersion relation ends up being linear in $c^{(2)}$; no approximation is needed here).

1. Growth rates without surface tension

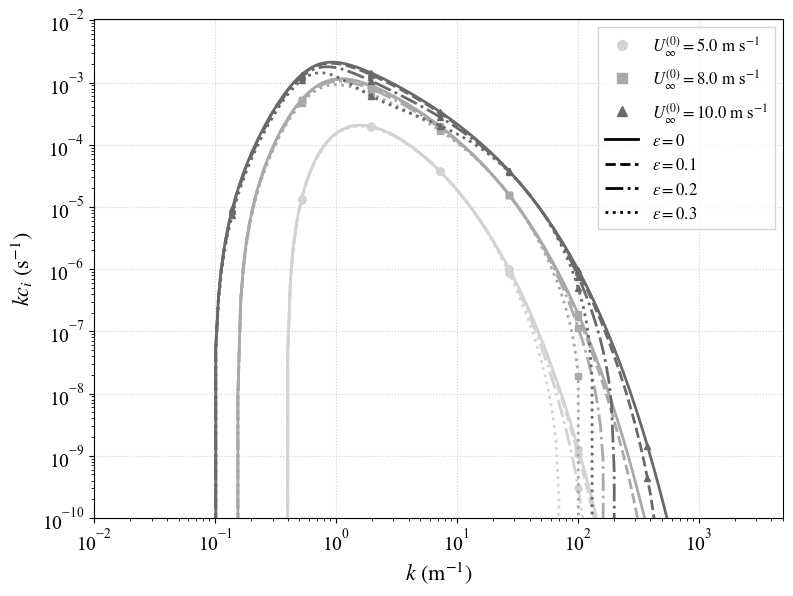
Modified growth rate as a function of wavenumber for several wave slopes and background shears, without surface tension. — **Figure 1.** Modified growth rate $k c_i$ vs wavenumber $k$ for four wave slopes $\epsilon$ and three far–field wind speeds $U_\infty^{(0)}$, with no surface tension. The solid curves ($\epsilon=0$) show the Miles growth rate, while the other curves include the $\epsilon^2$ correction.

**Parameters:** Double-exponential wind profile with $U_s^{(0)} = 0$; $U_\infty^{(0)} = 5.0,\,8.0,\,10.0~\mathrm{m\,s^{-1}}$; $\rho_{\text{air}} = 1.25~\mathrm{kg\,m^{-3}}$, $\rho_w = 1025~\mathrm{kg\,m^{-3}}$; air-layer depth $h_{\text{air}} = 1~\mathrm{m}$, water depth $h_w = 0.54~\mathrm{cm}$; wave slopes $\epsilon = 0,\,0.1,\,0.2,\,0.3$.

The $\epsilon = 0$ curves show the Lagrangian formulation reproduces the classical growth rate at leading order.
As $\epsilon$ increases, the $\epsilon^2\,\mathrm{Im}\,c^{(2)}(k)$ term systematically reduces the growth, especially at high wavenumbers.
Larger $U_\infty^{(0)}$ corresponds to enhanced background shear, and when it and the wave slope are sufficiently large, there is also significant suppression at intermediate wavenumbers.
This is on a log scale; the growth reduction is quite substantial, up to nearly a 40% decrease in integrated growth.

The modified growth rate, once computed for realistic double exponential background wind (and ocean) velocity profiles, shows significant suppression of wave growth with increasing wave slope.

2. Growth rates with surface tension

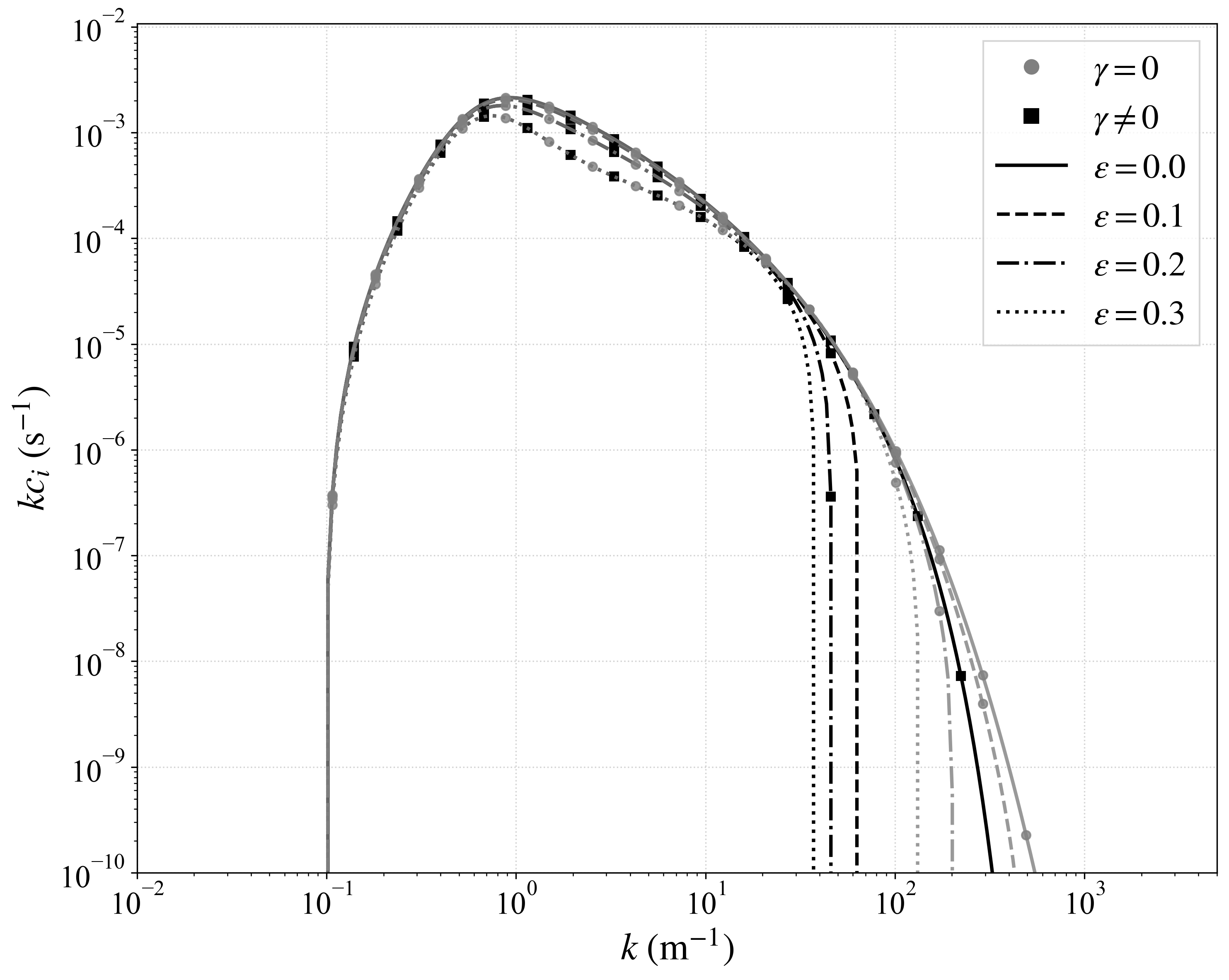
Modified growth rate as a function of wavenumber including surface tension, for several wave slopes. — **Figure 2.** Modified growth rate $k c_i$ vs. wavenumber with (black) and without (grey) surface tension. All curves use $U_\infty^{(0)} = 10.0~\mathrm{m\,s^{-1}}$.

**Parameters:** Same wind and density parameters as panel 1; far–field wind $U_\infty^{(0)} = 10.0~\mathrm{m\,s^{-1}}$; surface tension $\gamma = 7.2 \times 10^{-5}~\mathrm{m^3\,s^{-2}}$ (or $\gamma=0$); wave slopes $\epsilon = 0,\,0.1,\,0.2,\,0.3$.

The same growth suppression appears even when surface tension is included; it is not a competing or oveerriding effect
While intermediate wavenumbers affected by the modified growth rate have the same growth whether surface tension is included or not, the highest wavenumbers are significantly impacted by capillary effects, and the impact also increases with wave slope.