The Role of Lagrangian Drift in the Generation of Surface Waves by Wind

Authors

Lulabel Ruiz Seitz¹, Mara A. Freilich^{1, 2}, Nick Pizzo³

Institutions

¹ Division of Applied Mathematics, Brown University
² Department of Earth, Environmental, and Planetary Science, Brown University
³ Graduate School of Oceanography, University of Rhode Island

Background

Miles Theory

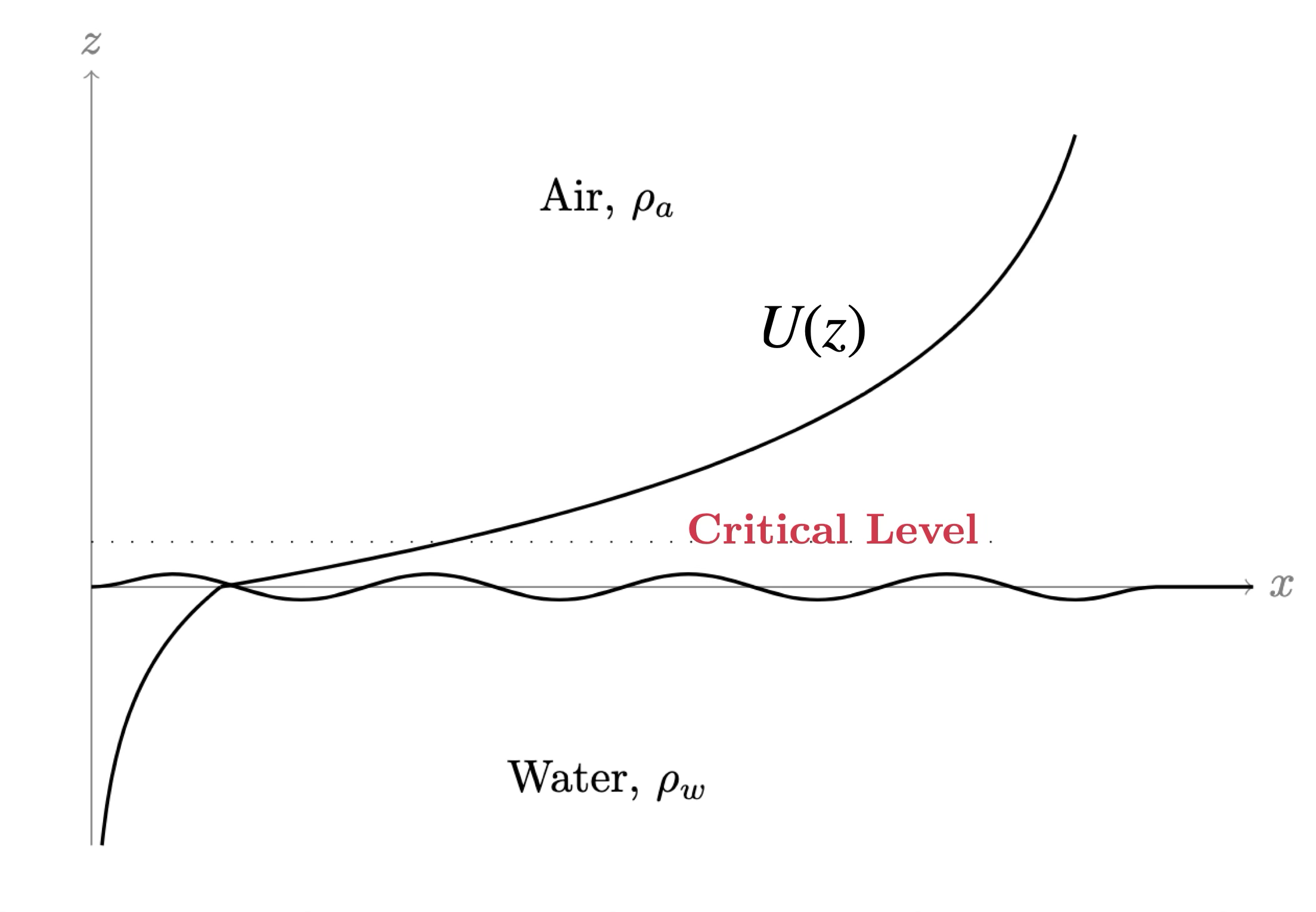
Miles' (1957) original theory for wind-wave generation finds that an instability corresponding to wave growth arises when the phase speed of an initial sinusoidal disturbance matches the background wind velocity at some height.

Lighthill Argument

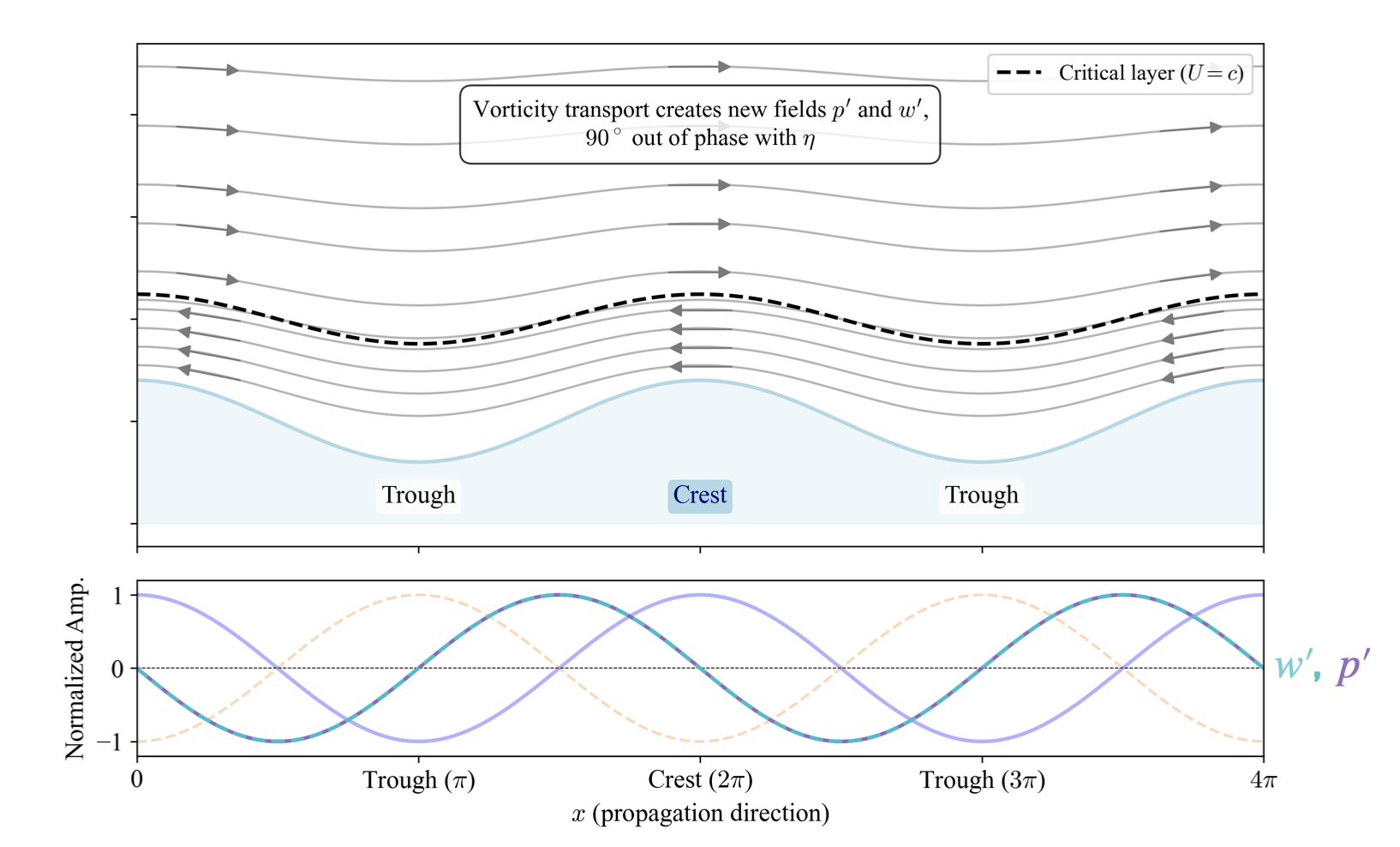
The physical interpretation behind the mechanism proposed by Miles was given by Lighthill (1962), mainly through a parcel argument. It thus involves the (mean) velocity a parcel actually experiences, the Lagrangian drift.

Overview of Our Work

Graphical abstract showing Lagrangian drift concepts

A parcel argument given by Lighthill (1962) is the basis of the physical understanding of the mathematical framework established by Miles (1957); this suggests the actual velocity experienced by a parcel is central to wind-driven wave generation.

Yet, the mean particle (Lagrangian) velocity and the mean Eulerian velocity used in the math differ by the Stokes drift:

$ \overline{\mathbf{u}}_L = \overline{\mathbf{u}}_E + \mathbf{u}_S. $

This drift scales with the square of wave slope (or amplitude). Thus, Lighthill’s picture aligns with Miles’ math at leading order, but the correspondence breaks down at higher orders.

To address this, we re-derive Miles’ analysis fully in the Lagrangian frame, through third order in the wave slope.

Methods

The Math (Single) The Math (EP) The Math (LP)

Results

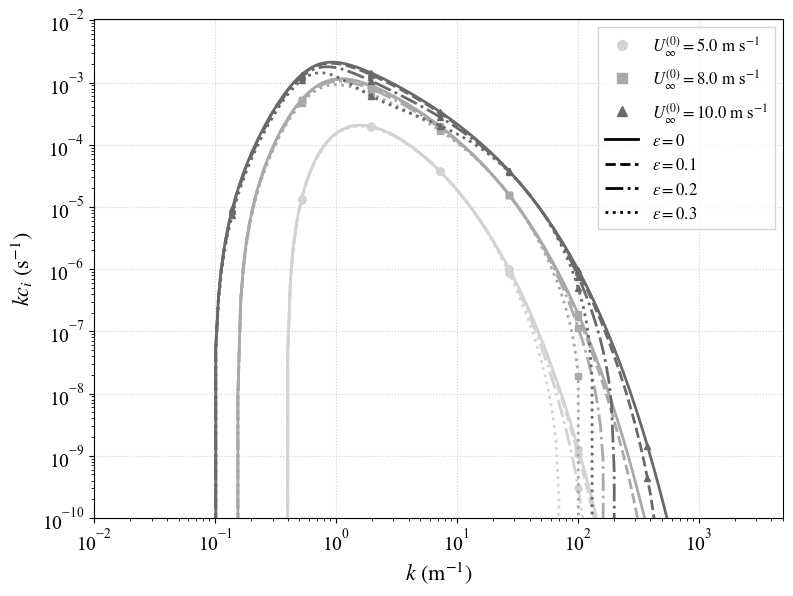
1. The wave-induced mean flow significantly modifies wave growth rates.

The leading-order correction due to the presence of the wave-induced mean flow significantly suppresses growth at high wavenumbers in all cases, but also at intermediate wavenumbers when the background shear and wave steepness are sufficiently large.

In the realistic double exponential background profiles tried, the integrated suppression could be nearly 40%.

Modified Growth Rates

2. Momentum budget depends on the Lagrangian mean velocity.

Specifically, the difference $c-U$ modulates the integrated momentum fluxes. Since $c=U$ at leading order but not necessarily higher orders, this supports that a detuning of the resonance due to the wave-induced flow may explain the suppression of wave growth.

Momentum Budget

$ \frac{\partial}{\partial t} \displaystyle\int_{0}^{b_c} \mathcal{J} \,\dot{x}\,\mathrm{d}b $ $ + $ $ \frac{\partial}{\partial a} \displaystyle\int_{0}^{b_c} p\,z_b\,\mathrm{d}b $ $ = $ $ \rho_0 g z\,\dot{z}\Big|_{b=0}^{b=b_c} $ $ - $ $ \tfrac{1}{2}\rho_0 \big(\dot{x}^2+\dot{z}^2\big)\dot{z} \Big|_{b=0}^{b=b_c} $ $ + $ $ \rho_0 f(b,t)\Big|_{b=0}^{b=b_c} $

Hover or tap a term in the equation to see its role in the momentum budget.

$ p = \rho_0\left[ -g z + \tfrac{1}{2}\,\underbrace{(c-U)}_{\text{total relative speed}} \big(\dot{x}^2+\dot{z}^2\big) + f(b,t) \right]. $

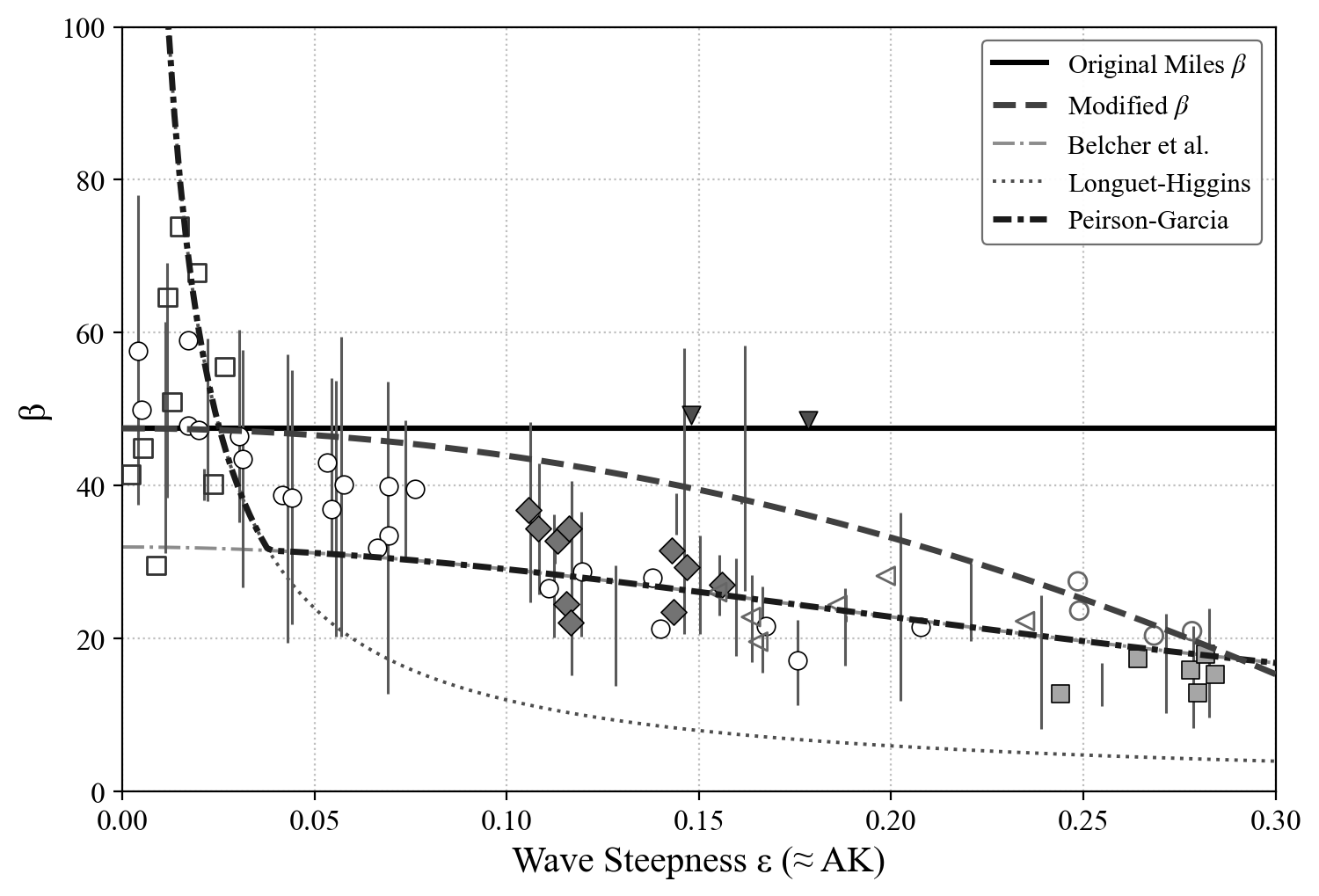
3. The predicted growth rates give a new explanation for experimental findings.

A collection of growth rates from wave tank experiments compiled by Peirson & Garcia (2008) shows a decrease of growth with wave steepness.

When approximated for a logarithmic wind profile, our growth rates align well with those observed: providing a single, mathematical, non-empirical explanation.

Experimental Data

Implications & Future Work

Observational Data Shear Instabilities Other Processes

arXiv preprint